See also the layperson's introduction: Jumping frogs, squeaking bats and tapping woodpeckers and Watching ripples on crystals.
We have now extended our surface wave imaging technique to a square phononic lattice.
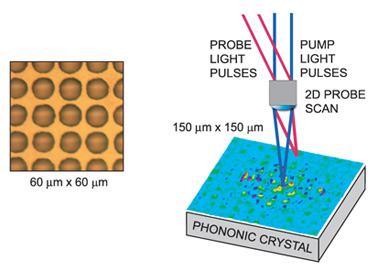
The image on the left shows the sample used: a microscopic array of holes, each 12 μm in diameter and 10 μm deep (1 μm=10-6 m), in a silicon substrate. The image on the right shows ripples generated by an ultrashort laser pulse striking the centre of the structure. The regular array of holes, forming a phononic crystal, scatters the sound waves.
Ripples on a square lattice of holes. Left: microscope image of part of the structure. Right: measurement setup and typical image. To animate click the image (970 kb movie).
Sound in these regular structures is forced into vibrational patterns known as Bloch waves. We can isolate different frequencies of these Bloch waves by filtering the movie (click the above image). Here is the vibration pattern at 305 MHz.
305 MHz Bloch waves on square-lattice phononic crystal. A 150 μm×150 μm region. To animate, click the image (450 kb movie).
The waves do not travel far from the centre—a symptom of the structure's band gaps at this frequency where no waves can pass.
Here is the vibration pattern at 382 MHz.
382 MHz Bloch waves on square-lattice phononic crystal. To animate, click the image (450 kb movie).
At this frequency the Bloch waves are standing waves, and are spread over a wider region of the sample.
Here is the vibration pattern at 458 MHz.
458 MHz Bloch waves on square-lattice phononic crystal. To animate, click the image (450 kb movie).
At this frequency the Bloch waves are collimated in the horizontal and vertical directions, due to phonon focusing, a phenomenon also observed in crystals.
We have also derived the character of the bands in this phononic crystal. Further studies of phononic waveguides and cavities are in progress. See also 'Watching ripples on phononic crystals,'
(For more details, see 'Dynamic visualization of surface acoustic waves on a two-dimensional phononic crystal,' D. M. Profunser, E. Muramoto, O. Matsuda, O. B. Wright, and U. Lang, Phys. Rev. B 80, 014301, 2009)