
一般の方向けの研究案内:パチャパチャ蛙、キーキーこうもり、トントンきつつきと結晶の波紋を見るのページもご覧ください。
平行な棒を並べ、間も別の物質で埋まっている格子があるとします。もし平らな格子に点波源を付けたら、波はどの方向に進むでしょうか? このバイキングのヘルメットの形はその道しるべです。詳しくは後述します。
クリックすると動画が見られます。(100 MBの英語の説明の動画です。クリックで見れない場合は、一度ファイルに保存して別のムービープレイヤーを試してください。)
私たちはミクロな格子上の音波の実験をしました。このような構造は、「フォノニック結晶」と呼ばれ、その音響的な性質が空間で周期的に変わるように作られています。 私たちの格子はシリコン板の上に幅2 μmの銅とシリカガラスの細片が順に並べられて作られています。さらに表面は金膜で覆われています。
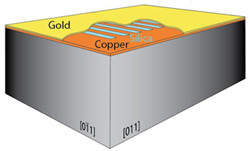
試料:幅2 μmの銅とシリカガラスの細片でできた格子。
私たちは、レーザーパルスを150 μm×150 μmの領域の中心に繰り返し当てました。周波数ごとの解析をしてみましょう。低い周波数では、だいたい円形の波紋が見えます。実際これは理にかなったことです。というのも、この周波数の音波の波長は約10 μmで、格子の周期よりも十分に大きいです。それで、音波は実効的には格子を感じることができないと言えます。 しかし、高い周波数では、私たちは面白いXの形をしたパターンを見ることができます。
格子上の点波源からの表面音響波の周波数フィルタしたイメージ。クリックすると、534 MHzの時間領域の実験データのアニメーションが見れます。(410 kBの動画です。)
次に、このイメージの中の音波の波長と速度を解析していきましょう。二つの重要な空間があり、それぞれ波数空間(フォノニック結晶中の波紋を見るをご覧ください)と群速度空間と呼ばれています。
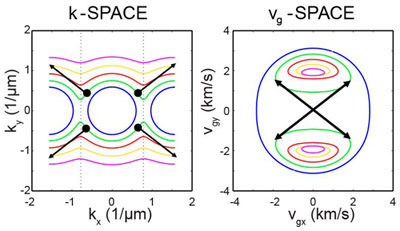
私たちの格子での周波数ごとの波数空間と群速度空間を示すモデル。
波数空間のある指定した周波数で、x方向とy方向について波長の逆数もしくは波数をプロットします。右に示す群速度空間では、音波パルスのの速度をプロットします。この近似的な解析的アプローチにおいて、低周波数(青い曲線)は両方の空間で丸まった形をしています。これは、波紋がおおよそ円形であることを意味します。
周波数が高くなるにつれ、水平方向に波が進むことのできないバンドギャップにあたり、波数空間では円の端が開きます。また、これは群速度空間では二つの円を生じさせます。 波数空間では、波は曲線の折れ曲がり点の近くで曲線に垂直な方向にとても強く進みます。群速度空間では、これは二つの円の接線が重なる点に対応します。これによって、イメージで見えたXの形となります。
もしすべての周波数を一緒に見るとすると、群速度空間は次のようになります。
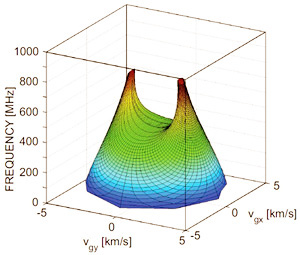
私たちの格子の音響特性を周波数ごとに表す群速度空間表記。
これで、バイキングのヘルメットとの関係がわかりました。これらの先端のとがったパターンは火面(コースティックス、caustics)と呼ばれます。コーヒーカップの中で、この現象の光の場合が見えます。また、音波を自然界の結晶上で発生させた場合にも見ることができます(結晶の波紋を見るをご覧ください)。よって、格子上で点波源によって生み出されたXのパターンはバンドギャップに関係した火面によって生じたといえます。この効果は様々な空間的周期構造で見ることができ、また音波に限ったことでもありません。例えば電磁波や水の波でも起こります。
より詳しくは、論文 'Point source in a phononic grating: stop bands give rise to phonon-focusing caustics,' I. A. Veres et al., New J. Phys. 2012をご覧ください。