
See also the layperson's introduction: Jumping frogs, squeaking bats and tapping woodpeckers and Watching ripples on crystals.
Here is a grating of parallel bars. If you put a point source of waves in a flat grating, which way will the waves go? The shape of this Viking Helmet is actually a clue. More of that later.
Click to see the video! (90 Mb movie)
We experimented with sound in microscopic gratings. Structures like this are called "phononic crystals", whose acoustic properties have been engineered to vary periodically in space. Our grating is made of tiny copper and silica strips of width 2 μm on a silicon slab, and this is coated with gold.
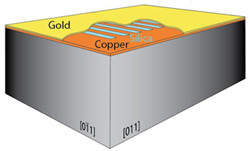
Sample: a grating of copper and silica glass with 2-μm wide strips.
We fire laser pulses repetitively at the centre of a 150-micron-square area. Let's analyse at different frequencies. At low frequencies, we see roughly circular ripples. Actually this is reasonable, because the sound wavelength is about 10 microns, much larger than the grating bars, so the sound effectively doesn't see the grating. But at high frequencies, we see this interesting X shaped pattern.
Frequency-filtered images of surface acoustic waves generated at a point on a grating. To animate at 534 MHz in the time domain, click the image (410 kb movie).
Now let's analyse the sound wavelengths and the sound speeds in these images. There are two important spaces called k-space (see Watching ripples on phononic crystals) and group-velocity space.
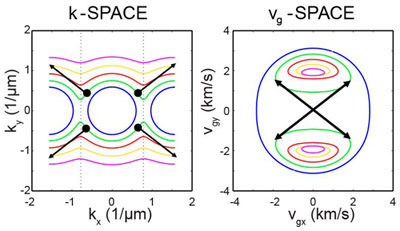
k-space and group-velocity space representations of a model of our grating at different frequencies.
For a given frequency in k-space, we plot the inverse of the wavelength, or rather the wavenumber, in the x and y directions. In group velocity space, shown on the right, we plot the speed of a sound pulse. In this approximate analytical approach, at low frequencies (blue curves) we get rounded shapes in both spaces. This means the ripples are roughly circular.
As the frequency increases we hit a band gap in the horizontal direction, a direction waves can't travel, visible through the opening of the circles in k-space. And this makes two circles in group velocity space.
In k-space waves go very strongly perpendicular to the turning points in the curves. In group velocity space, this corresponds to joining the tangents of the circles. This produces the X shape we saw.
If we see all frequencies together, group velocity space looks like this.
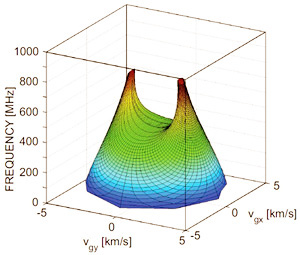
Group-velocity space representation of a model of our grating at different frequencies.
So now you see the relation with the Viking Helmet. These spiky focusing patterns are called caustics. You can find optical versions of them in coffee cups, and also when you generate sound waves on real crystals (see Watching ripples on crystals). So a point source in a grating produces an X pattern caused by caustics related to the band gap. This effect should also be seen in a variety of spatially-periodic structures, and is not just confined to sound. It would occur with electromagnetic or water waves, for example. See 'Point source in a phononic grating: stop bands give rise to phonon-focusing caustics,' I. A. Veres et al., New J. Phys. 14, 123015, 2012.